2. 纯律中的所有音程都是由2,3,5这三个倍数关系的组合构建出的。 3. 在纯律中,纯五度和大三度是一个音高与它的3/2倍和5/4倍之间的音程距离。 4. 其他的音程都可以由纯八度、纯五度、大三度这三个音程的叠加或相减推算出来。 0. 给初学者的阅读建议:前三课的重点是音程的概念,第一课中介绍了纯八度,第二课定义了大三度和纯五度,而第三课带大家认识了半音、全音、以及纯八度中的“度”,这三个音程单位。
第一堂课,我们介绍了八度这个音程概念。音程就是音与音之间音高频率上的距离——更确切的说是倍数关系。音程的大小可以用倍数的大小来衡量。而八度音程则代表了两个音之间频率是二倍关系。
这一讲,我们来讨论一下音乐家是如何在一个八度里面挖掘出好听的音程关系的,即Do Re Mi Fa Sol La Ti这些唱名和它们之间的音程是怎么被定义出来的,并由此为下一讲引出“十二平均律”这个概念做铺垫。 今天的内容会涉及一些初高中数学。但是在进入算数前,大家要知道一个现象。人耳除了能够体会八度之外,对有简单整数倍关系的音高频率组合会感到相对协和,而对复杂倍数关系的音高频率组合会感到相对的不协和。物理学上,由简单倍数关系的频率组成的波,其在物体上的振动模式更为规则,而这种振动的规则性对人来讲就比较悦耳。倍数越简单就越协和,因此我们可以利用这个规则来挑选八度中的音程关系并定义唱名。 1. 八度、五度与三度
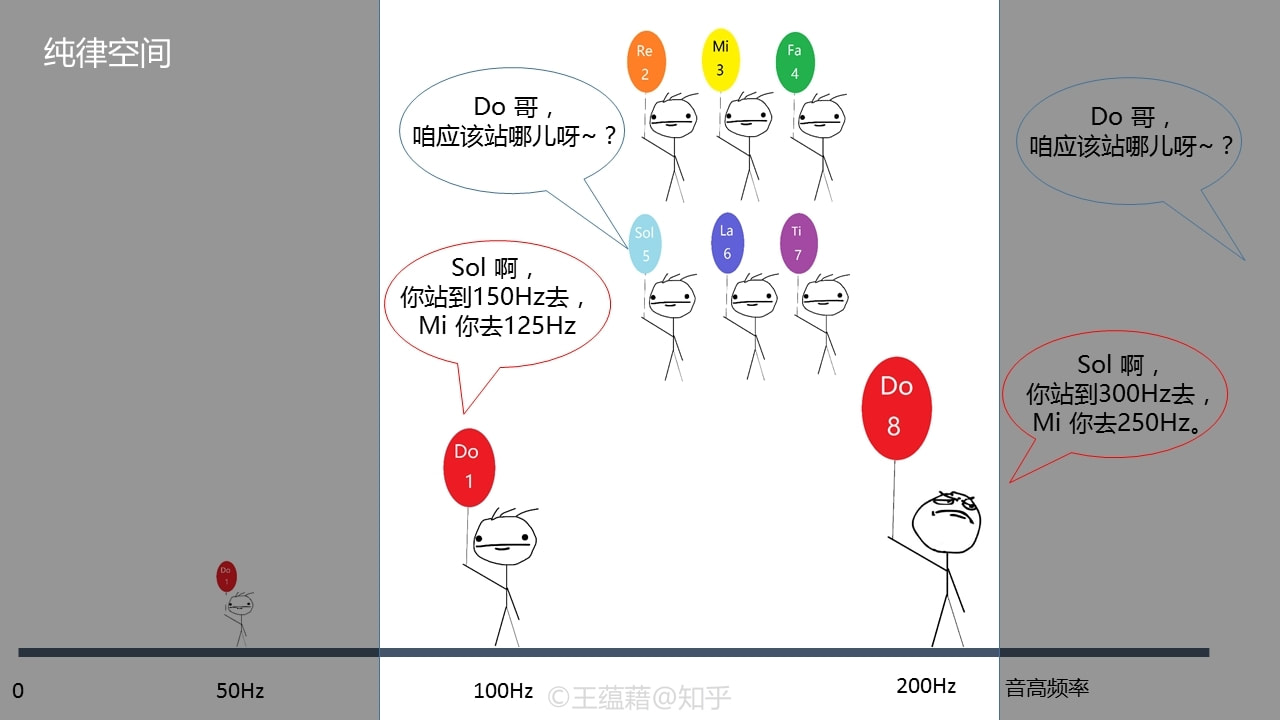
现在已经知道了,某个音高Do[1],它频率的两倍或四倍的音还是Do,分别是高了一个或两个八度的Do[8]和Do[15]。通过八度是无法产生新的唱名的,它只能让我们在同一个唱名上面上蹿下跳。因此如果想要定义出新的唱名出来,我们需要探索其他的简单整数倍数来构建音程。顺理成章地,音乐家把目光瞄准了三倍和五倍关系。
不过,首先会遇到一个麻烦:我们想要在八度的范围内来定义新的唱名和音程,但三倍、五倍音高显然已经超出了一个八度的范围。幸亏,根据八度的二倍关系,在原有整数倍数上任意地乘以或除以很多个两倍之后,依然会得到同样的唱名。也就是说,Do[1]的三倍音高与Do[1]的3/2倍音高将会是同一个唱名。因此,我们可以用3/2倍来定义这个新的音程及唱名。 音乐中,我们把这个3/2倍的音程定义为纯五度(以下简称五度),并将Do[1]向上一个五度音程得到的唱名叫做Sol[5]。相应的,Do[1]的三倍音高则为Sol[12],比Sol[5]高了一个八度。 基于二倍关系的纯八度是最协和稳定的音程,以至于它听上去显得过于冷硬单调。而基于三倍的纯五度音程,它的协和度仅次于纯八度,听感依旧稳定的同时,却多了一丝温度。 我们可以看到,五度是由三倍关系组合八度的二倍关系获得的新音程。类似的,我们也可以用五倍关系与八度来构建另一个新的音程。 于是,我们把5/4倍的音程定义为大三度,将Do[1]向上一个大三度得到的唱名称做Mi[3]。相应的,Do[1]的五倍音高是Mi[17],比Mi[3]高了两个八度。大三度的协和稳定性比五度又要次一些了,但是牺牲所换来的是它听起来更具有色彩感。 (关于为什么这两个新的音程要叫做“三”度、“五”度,下一小节就会看到原因。这里也不用纠结“大”和“纯”是什么意思,第四讲会细解释) 音乐其实是游走于协和与不协和之间的艺术,并不是越协和就越好听。协和的音程能带来稳定的体验,而不协和的音程却能为乐曲增色。对大脑来说,音乐太过稳定了就会很没劲,而太过“粗糙”不协和了则成了噪音。就跟烧菜一样,协和的音程就是音乐里的饭菜,不协和的音程就是油盐酱醋,一般人烧菜都会放一些佐料来调味。适宜的酱料能开胃消食,但放多了容易齁住,放少又会没胃口。当然,有的人重口味一些,有的口味比较淡,每个人的音乐的品味也各不相同。在协和与不协和的两级中找到平衡是音乐能给人带来好奇和愉悦感的秘诀。 虽然大三度已经开始变得不如八度和五度那么稳定了,但是从听觉上它还是太协和了,以至于如果一个音乐只用Do Mi Sol来作曲的话,若没有很丰富的节奏,恐怕大家都会无聊到睡着的。所以我们需要搜寻更多的佐料,即更多特色各异的音程关系,来往音乐食材里添加。 这一小节概括为一句话:二倍生八度,三倍生五度,五倍生三度。 2. 纯律
现在已经知道了,Do的频率乘以三倍和五倍可以形成Sol和Mi,这样我们就已经获得了三个独特的音。那如果想要定义出更多的音,我们是不是可以往更高的倍数上去找呢?
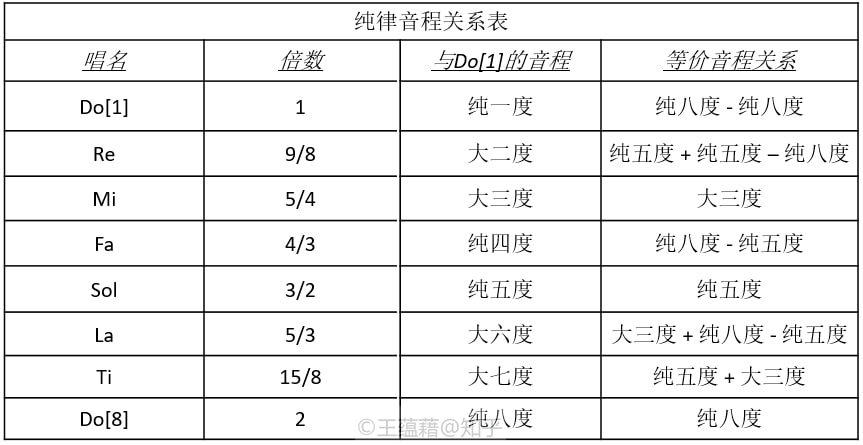
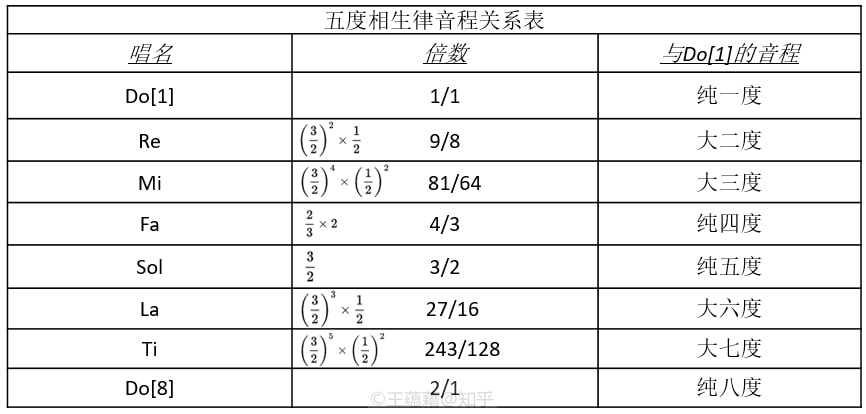
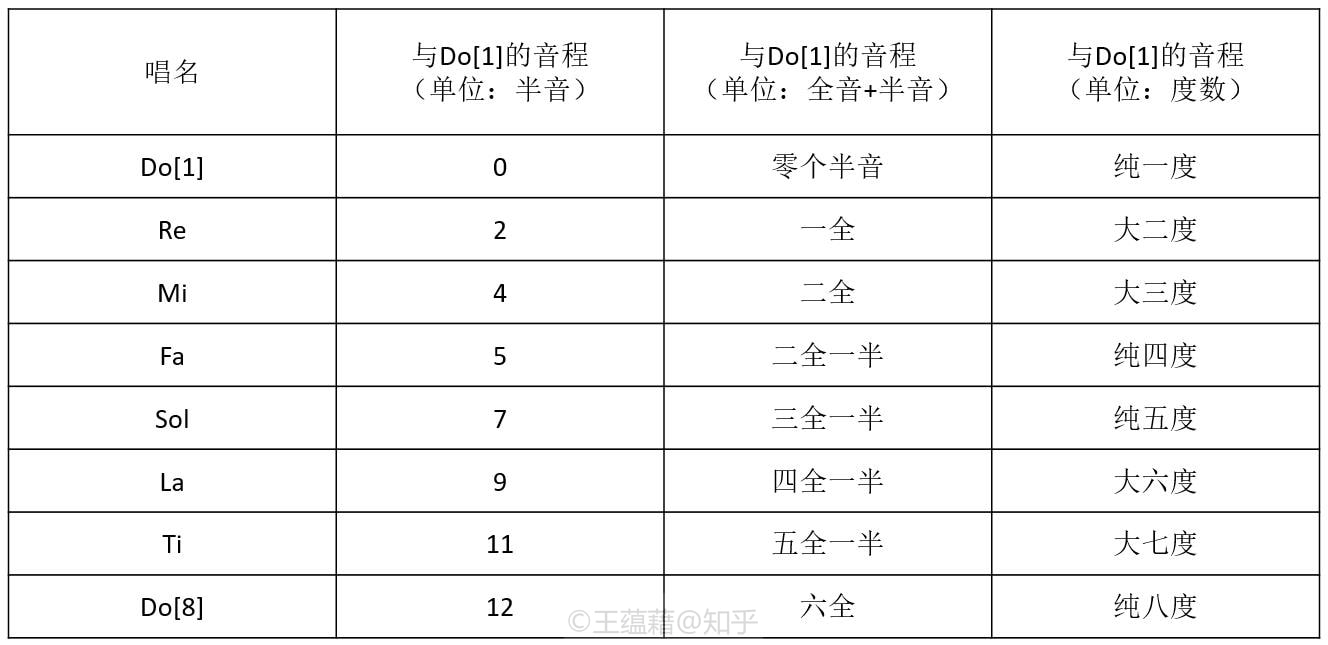
由于一个音的二倍四倍都是八度音,三倍六倍都是五度音,而五倍是大三度音,如果要按照正整数倍从小往大去找全新的音程关系的话,下一个选择就是七倍关系了。可惜的是,这个七倍音在当时的音乐家听来不是很协和,不适合邀请它加入。 那还有什么办法可以生成与Do Mi Sol待在一起会好听的音出来呢?何不就地取材,试着通过加加减减拼接组合这三个音程来形成新的唱名和音程呢? 音乐家们确实这么做了。仅凭借着两倍、三倍、五倍这三个简单倍数,他们定义出了一套完整的Do Re Mi Fa Sol La Ti的音程关系。这个以八度,大三度,和纯五度为基础衍生出音阶上音程关系的方法被叫作“纯律”。纯律是由弦乐上泛音列产生的律制,因其三度音与五度音这两个音程的倍数简单,它们组成的大三和弦最为纯正悦耳,故得名“纯律”。 下面是我整理的一张纯律音程关系表(注意音程倍数都是由2,3,5三个数字的乘除构成的):
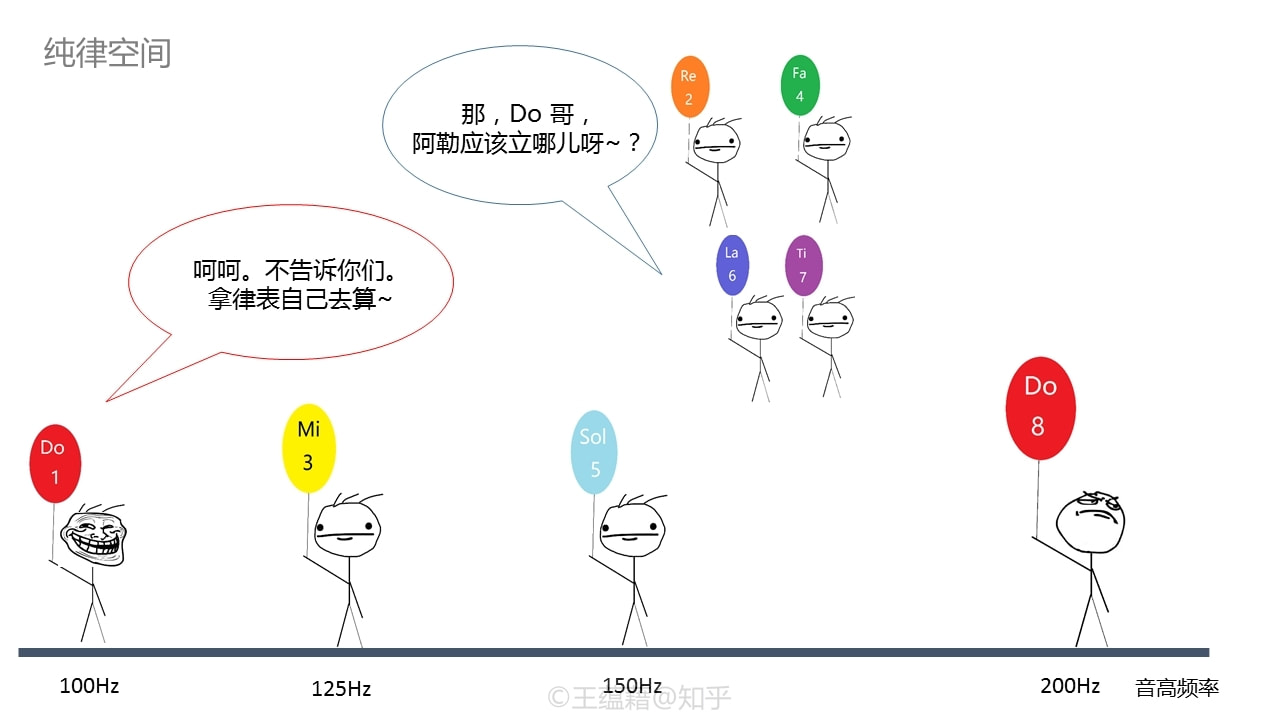
如表所示,我们在已有的Do[1]、Mi[3]、Sol[5]、Do[8]四个音之外,在八度内又划分出了Re[2]、Fa[4]、La[6]、Ti[7]四个音。一共是八个音,有七个独特的唱名,我们且称它们“唱名七兄弟”。从老大Do[1]出发,到其他七个音可以形成七个不同的音程。(算上Do[1]到它自己的音程,就是八个不同音程。)
由于Mi[3]和Sol[5]在七兄弟里排行老三和老五,这也是为什么我们把Do[1]到Mi[3]和Sol[5]的音程叫做大三度和纯五度。二哥Re[2]的音高是Do[1]的\(\frac{9}{8}\)倍,音程介于纯一度和大三度之间,叫做大二度。而介于Mi[3]和Sol[5]之间的四弟Fa[4]距离Do[1]的音程是纯四度,其它音程以此类推。
七个唱名的设计非常科学。一方面七个音的搭配已经足以构建出丰富的音乐性,很好的平衡了音与音之间的协和与不协和性;一方面相比细分出一百个唱名来讲,七个唱名的设计保证了一般人即使没有受过训练,也可以用耳朵区分两个音的高低不同。
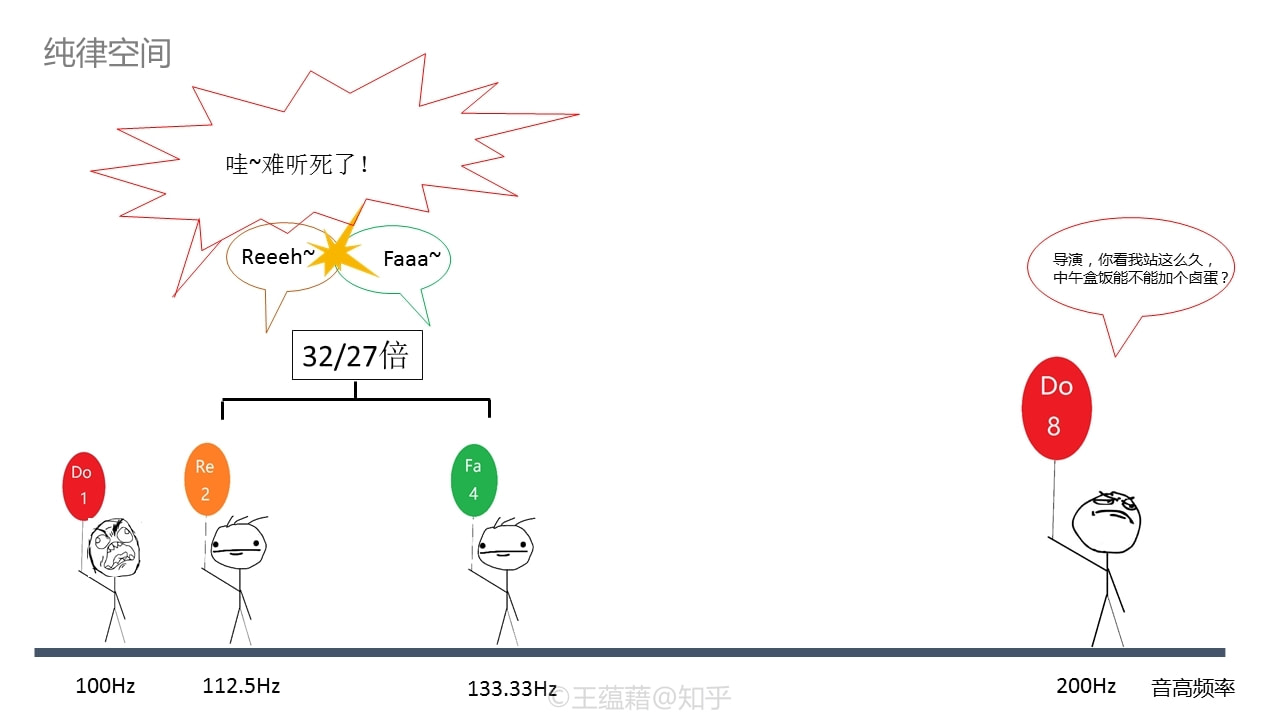
然而,纯律是有缺陷的。如果我们来比较一下Re[2]到Fa[4]的音程关系的话,会发现这个音程是一个远远比其他音程复杂的倍数关系\(\frac{4}{3}\div\frac{9}{8}=\frac{32}{27}\),更糟糕的是从Re[2]到La[6]的音程\(\frac{5}{3}\div\frac{9}{8}=\frac{40}{27}\),约等于1.481。大家将来会理解,音程不一定要从Do[1]向上数起,也可以从别的音算起。Re[2]到La[6]之间其实和Do[1]到Sol[5]一样,是一个五度的音程。纯五度本来的音高倍数应该是\(\frac{3}{2}=1.5\)倍,现在却偏离了1.23%。若在一个本来就不协和的音程上做微调那还好。但是,在本来极其稳定的五度上,细微的音程变化是相当明显的。这就造成以纯律定调的乐器在演奏某些音程时听上去会不协和。
这个问题早在纯律之前的五度相生律就存在了。五度相生律,古称三分损益律,是仅由八度和五度衍生出来的律制,所有的音程都是由二倍和三倍的数学关系组合出来的(见)。因此和纯律不同,五度相生律中大三度的倍数是81/64。虽然五度相生律让五度达到了最协和的音程倍数*,但它的大三度相比纯律听上去可就没这么纯正了!(点击可以观看五度相生律的视频讲解)
那么存不存在什么办法可以让八度内的所有音程都符合简单整数倍数关系,从而变得好听呢?
答案是:不存在!我们知道2,3,5都是质数,而质数之间是没有整数倍的,也无法通过乘除组成新的质数。但是,确实有一种方法,可以在不满足简单整数倍的情况下,让所有的音程之间都变得好听,这个方法就叫做十二平均律,是我们下一讲的话题。 总结一下,这节课我们介绍了三度和五度是如何被定义的,以及由此产生的纯律,纯律中其他的音程与唱名。下一讲会基于纯律的缺点进行改进,介绍十二平均律这个定律手法,以及平均律为什么会被广泛使用在钢琴吉他等乐器中。 P.S. 1. 这篇文章看完之后,除了可以尝试课后练习之外,强烈推荐大家点击下方链接进入音频演示区,用音频来直观地体验一下八度中每一个音程的协和与不协和感。你可以将它们与纯律表中的音程的音高倍数作对照,亲自感受倍数的简单程度与音程的协和性的关系。这对将来的学习大有帮助。切记,学习音乐,不能只学习乐理,同时也需要训练你的耳朵,听懂音乐,记住音乐,创造音乐。不然就沦为了纸上谈兵。 链接:【乐理101】3+. 十二,一个神秘数字引发的革命(辅助材料) 2. 纯律有不止一种,它是用小的整数倍数发展出的音律的集合。本文中特指的,用2,3,5三个质数作为基础的纯律叫5-limiting tuning(以最大的质数作为名称中的数字),翻译过来就是“最大的因数为五的调律”,只是纯律中的一种。而用2,3,5,7四个质数作为基础的纯律就叫7-limiting tuning。这样说来,五度相生律其实也是纯律的一个特例,用2,3两个质数为基础,因此也叫3-limiting tuning。 3. 五度相生律中有一个五度并不协和,降Re与降La,被称作“狼音程“”,Wolf interval。
Q1: Do[1]的5/2倍音高是高八度的哪个音,它的唱名是?那6倍音高呢,6倍音高和3倍音高之间是什么度数关系? Q2: 高八度的Fa[11],它的音高频率是原八度Do[1]的几倍?它的音高频率是原八度Fa[4]的几倍? Q3: 根据纯律的音程关系,请问Do[1]的9倍音高,15倍音高分别是什么唱名? Q4: Re[2]和Mi[3]之间的音程是什么倍数关系?
Q1: 如果Do[1]的频率是261.6Hz(中央C),那么请问Do[8],Do[15]的频率分别是多少?
A1: 分别是二倍523Hz和四倍1046Hz。(注意:高两个八度是四倍不是三倍)
Q2: 如果La[13]的频率是440Hz,那么请问La[6]的频率是多少?
A2: 低八度的La是220Hz。
纯五度:Perfect fifth 大三度:Major third 调律:Tuning 纯律:Just Intonation 五度相生律: Pythagorean tuning (毕达哥拉斯Pythagoras就是发现勾股定理的那位古希腊人,这个调音法据说是他最早提出的) 协和与不协和:Consonance vs. Dissonance 十二平均律:Equal temperament 泛音:Harmonic
对协和的感知应该是由「和弦中的音的泛音重叠多少」所决定的P.S. 当我们在弹奏钢琴或者吉他的一个音时,比这个音的频率高2,3,4,5...倍的声音也会混在这个音里面一同发出,这些音就叫做泛音。具体泛音的知识,我们将来会讲到。 2. 毕达哥拉斯怎么找到 Do Re Mi?
0 评论
2. 由于平均律中,相邻音高之间倍数是固定不变的,因此在转调上特别容易,只需将整体音高平移几个音程即可。纯律和五度相生律则不行。所以现代音乐多以十二平均律定调。 3. 由于等比的倍数关系,我们可以把音程的比例关系转化成整数关系,以半音程为最小单位刻度来衡量音程距离。 4. 音程常用单位有半音,全音,以及度。两个半音程组成全音。而多个半音可以组成不同的度数,用度数来讨论比较大的音程相比用半音程更加方便。 们介绍巴赫时,除了提到他是巴洛克时期的顶峰人物,一生“多产”之外(不光是作品多,而且他有二十个孩子),常常会带出一个音乐名词叫十二平均律。平均律的诞生在音乐史上意义重大,它是欧洲音乐摆脱中世纪中古调式,走向现代音乐中能够随意变调的一把钥匙。你能想象在平均律之前,每一种曲调的调音都不同,乐曲想转一个调是多费周章的一项工程吗?同样,平均律对中国人来说也是可以和四大发明一样,令国人自豪的一个创造。历史上记载十二平均律的推算者是明朝的朱载堉。不同于圆周率等其他中国早期数学发现,朱载堉在平均律的创始人地位是在世界上被公认的。怎么样,你是不是对十二平均律感到好奇了呢?今天就来为你揭开十二平均律的奥秘。
上两节课,我们普及了八度、五度和三度这三个存在简单整数倍关系的音程,以及由这些音程推演出来的纯律和五度相生律。在文末讲到,纯律和五度相生律并不完美,八度中并不是每一个唱名之间的音程都是协和的,因此需要探索一种更优的解决手法。
现在我们知道,想要在八度中定出一个让Do Re Mi Fa Sol La Ti都感到开心的音程和音律,曾经是多么令音乐家困扰的事情。好在,十二平均律出来拯救世界了! 1. 什么是十二平均律
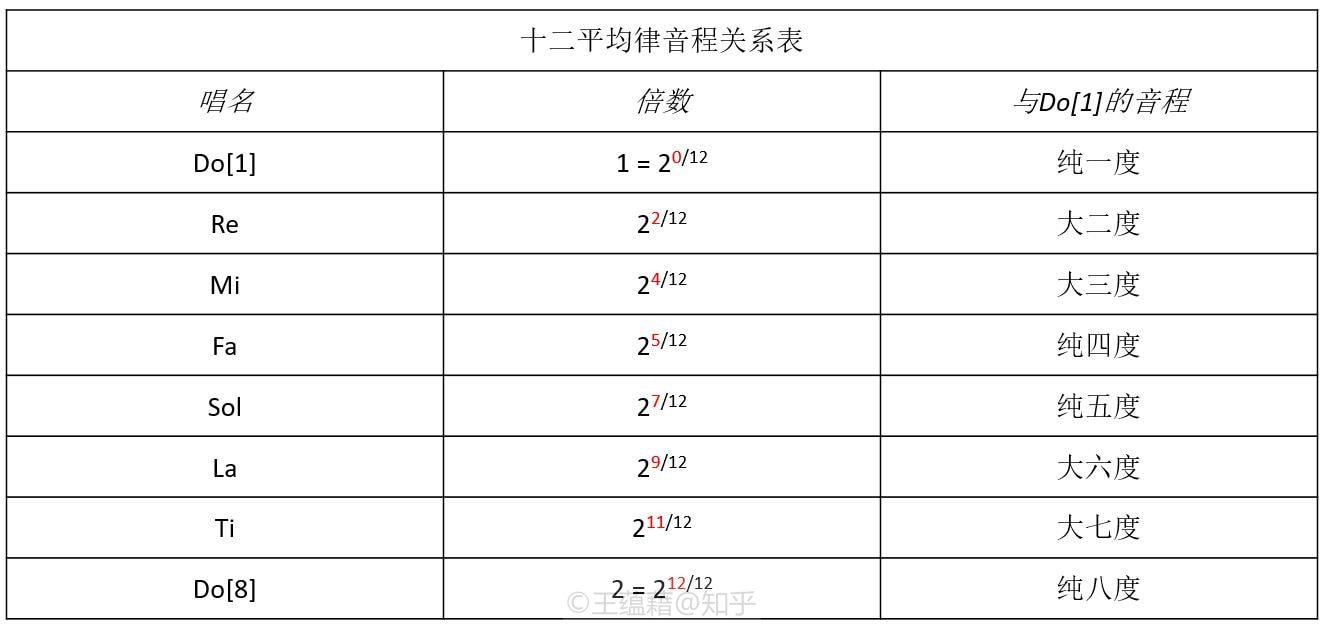
十二平均律,或平均律, 是将八度的二倍音程等比例地划分为十二份的定律方式。它让每一个临近的音在音程上都是同样的倍数关系。这每一个音和主音Do[1]组成的音程的倍数关系分别是\(2^{n/12}\),n=0到12。(当n=12,倍数正好是二倍即纯八度,它对应的音名和当n=0时纯一度上的音是一样的。所以去掉12,从0数到11正好产生十二个不一样的音名。)
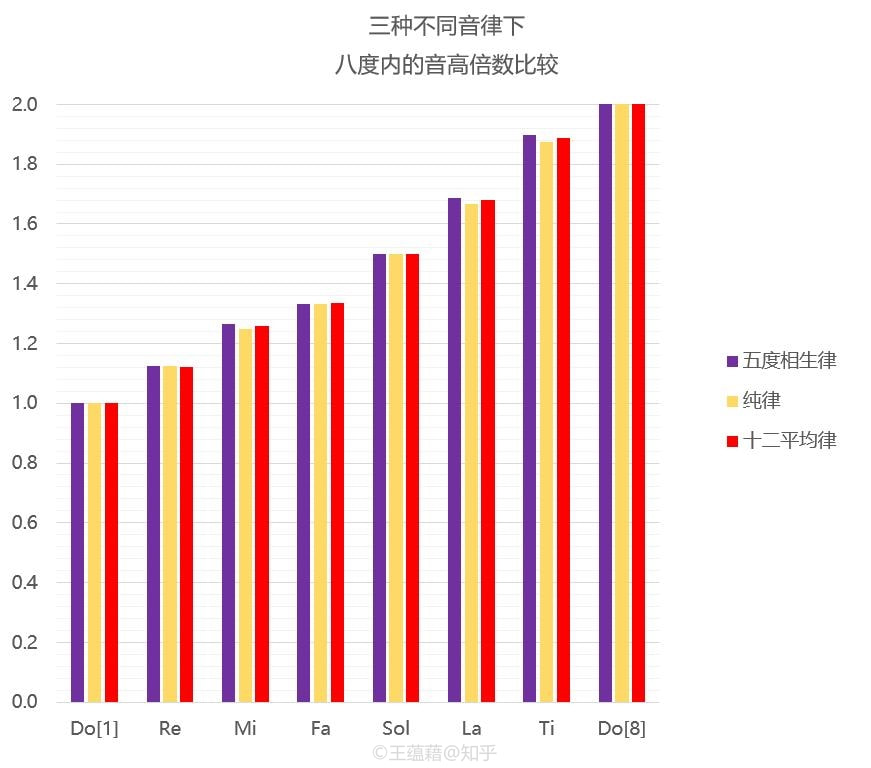
虽然十二平均律是人们通过幂运算凭空创造出来的数学概念,这种律制中的音与音之间并没有正整数倍关系(除了八度),但是它的十二个音中恰好有七个音,在音高倍数关系上和纯律以及五度相生律中的Do Re Mi Fa Sol La Ti极为接近——以至于如果我们用十二平均律来定义音程的话,耳朵并不会明显地察觉到异样。七个音与Do[1]之间的音程分别近似于以下这些倍数关系:
上图比较了在三种不同音律定义下,每个音在音高上的差异。我们发现十二平均律这个人工产物生成的音程竟然和五度相生律以及纯律里有自然倍数关系的音程是那么的接近,怪不得耳朵不会听着觉得古怪!(或者反过来说,我们的耳朵竟然能够自动将复杂的倍数关系约成简单的倍数关系来消化感受!)
平均律虽然轻微地牺牲了遵循简单整数倍这个让音程听着协和的自然规律,使每个音都稍稍变得不纯,但却换得了极大的好处。首先,它使得音程不再会在纯五度音程上出现不协和的问题。平均律的纯五度倍数是\(2^{7/12}=1.498\),非常接近纯律中的\(\frac{3}{2}\),误差只有0.1%。相比上一篇文章中纯律里出现过的\(\frac{40}{27}\)倍音程和1.23%的误差,要小了十倍。平均律中的大三度偏离纯律的程度相比五度要大,但其表现尚佳,优于五度相生律。
其次,平均律保证了音程倍数关系永远是固定值。比如说,从Do[1]到Re[2]之间是大二度关系,音高比例为\(2^{2/12}\approx1.122\)。而Re[2]到Mi[3],以及Fa[4]到Sol[5],这两组音之间同样是大二度关系,他们的各自的比例也是\(2^{2/12}\),倍数不会随着起始音位置发生改变。而这在纯律上是做不到的。根据上一节课后练习第四题,我们知道纯律中Re[2]和Mi[3]之间的音程是\(\frac{10}{9}\approx1.111\) 倍的关系,与Do[1]到Re[2]的\(\frac{9}{8}=1.125\)倍稍有不同。 不仅大二度是这样,在平均律中,任何相同的音程度数都不会随着音高的升降而改变。将调里面的所有组成音都升高或降低几度时,调内音程的倍数关系是不会更改的。因此,使用平均律的乐器可以轻松地完成转调的工作,而不需要每次为不同的调来调整音高的设置了。(调是什么,怎么理解转调,我们会在第六课详述。)
由于其实用性,平均律的诞生席卷了一场音律革命,把纯律和五度相生律等等都赶进了角落里。可为什么古人会想到把八度划分成十二等分呢?由五度相生律推算出的第十二个音,它和起始音高的音程约为两倍。而二倍即一八度。可能就是这个原因,使得当时的人们想到通过把十二个音进行细微的调整来构建八度了。
十二真是个神奇的数字!谈起十二这个数字时,我们还会想到什么?一年有十二个月份,一英尺有十二个英寸,一个钟表有十二个刻度。这或许是上帝的神来一笔,或许一切都只是巧合。但无论如何,由十二这个数字推算出来的平均律特别好用。 2. 半音、全音与度数
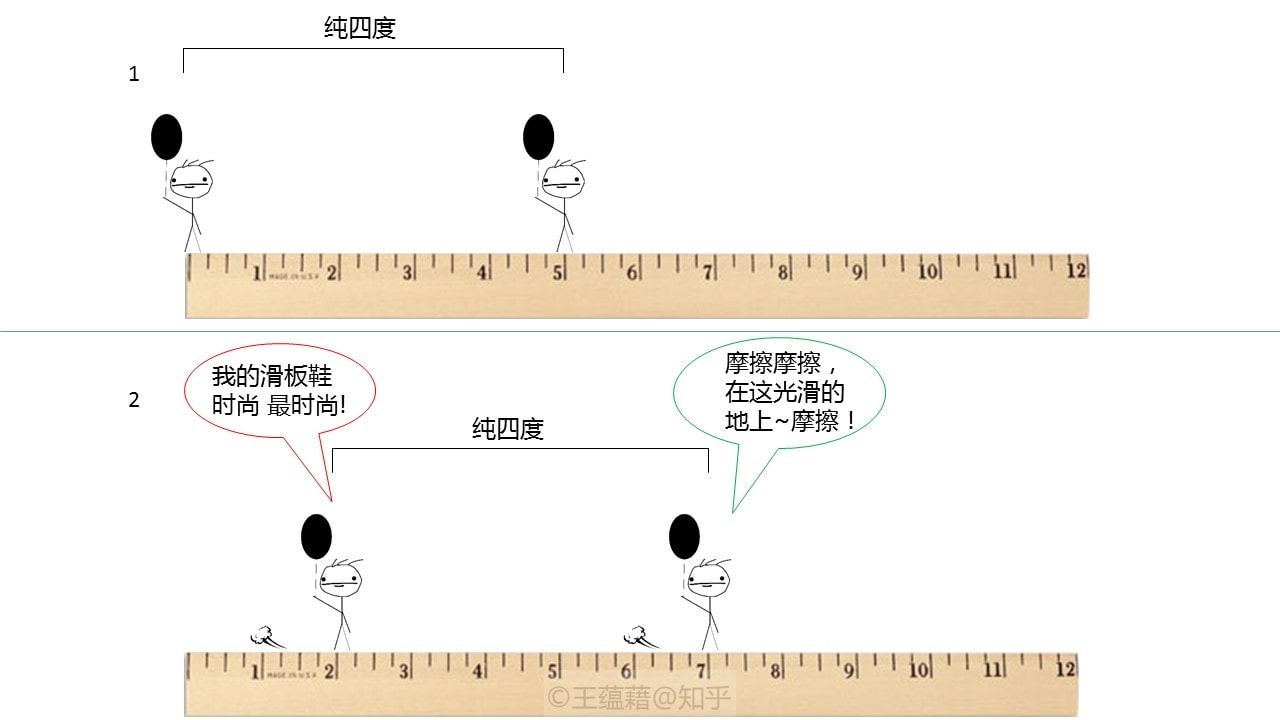
现在到了见证奇迹的时刻!正因为十二平均律的等比关系使音阶变得“平均”,我们从此再也不需要用倍数去演算音程了,而是改为直接用整数刻度来衡量音程的“距离”。我们把平均律的十二个音中,相邻的两个音之间的音程距离(\(2^{1/12}\)倍)叫做半音程,简称半音。半音是现代音乐中衡量音程的最小刻度。就好像一把尺子上的刻度一样,一个半音就像是1cm这个刻度,而一个八度的距离是12个刻度也就是12个半音。因此,我们可以重新定义八度,八度就是相差十二个半音的音之间的音程。同样,五度的定义就是七个半音程。以此类推。从此,我们在音乐上只需要用小学数学的加减法,就能解释一切乐理了!
(给理工科人的解释:我们通过把音程倍数取 log_2 将音高频率间的指数关系转化成了线性关系)
知道了半音这个音程概念,我们可以将之前所有的音以半音为刻度来度量。比如说Do[1]到Re[2]之间的大二度,是由两个半音组成的。Do[1]到Sol[5]之间的纯五度,是由七个半音组成的。Mi[3]到Ti[7]之间差了11减4也是七个半音,因此它们之间也是纯五度的关系。
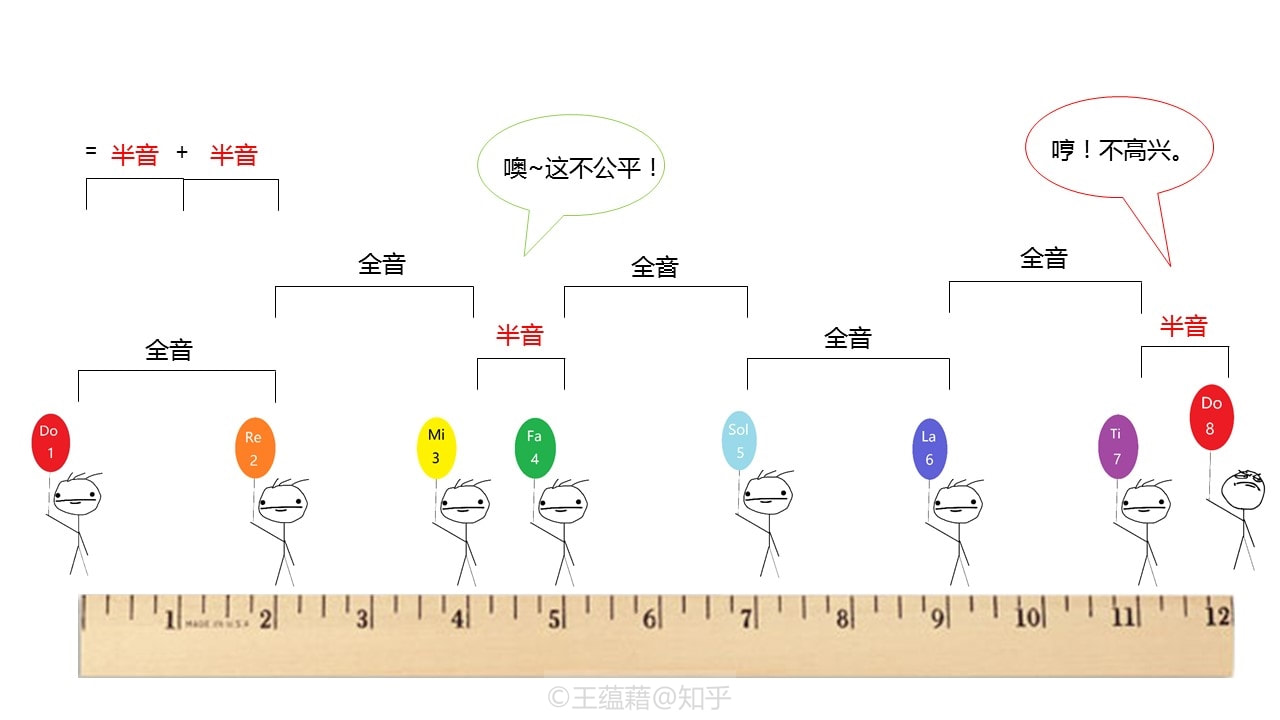
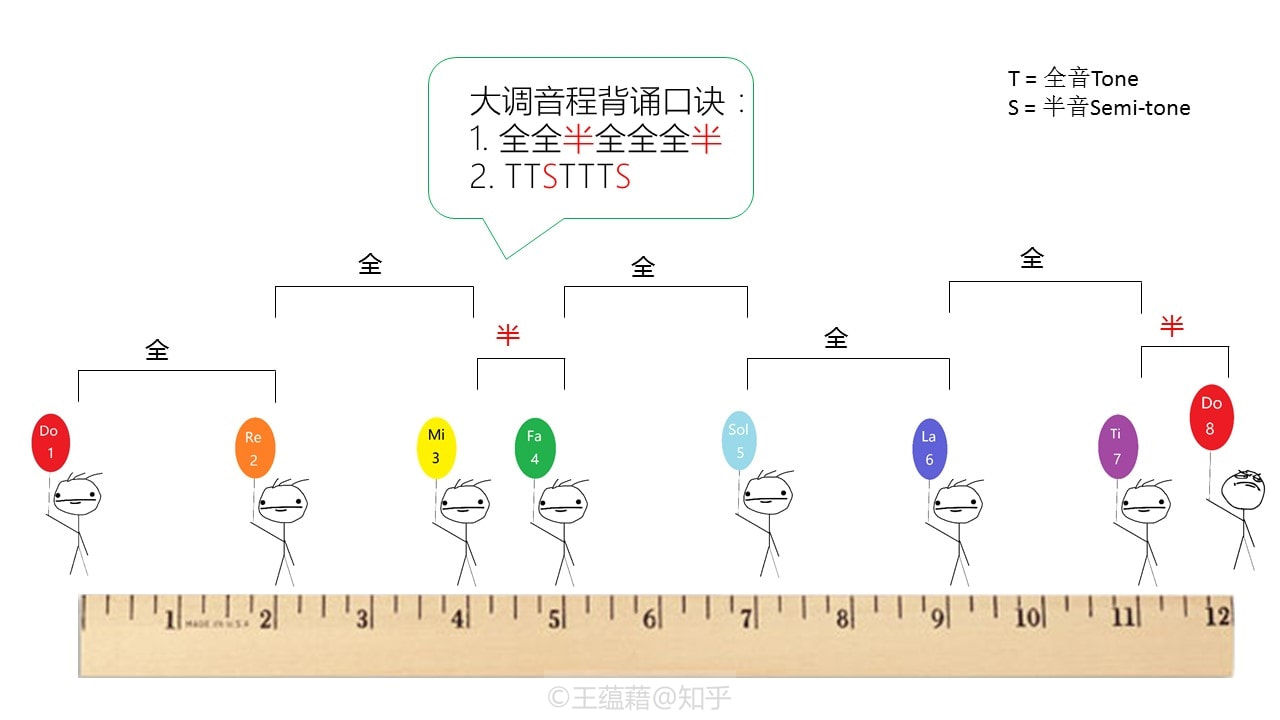
比半音大一点的单位叫全音程或全音,全音是由两个半音程叠加组成的,等价于大二度。仔细的朋友已经发现,Do[1] Re Mi Fa Sol La Ti Do[8]相邻两个音之间音程只有两种关系,一种是全音,一种是半音。Mi[3]到Fa[4]以及Ti[7] Do[8]之间都是半音,而剩下相邻音之间则都是全音。(请务必牢记这个规律!)因此,有些情况用全音与半音一起描述音程比直接用半音来得更便捷。 另外一种讨论音程的单位是度,度用来描述比半音和全音要大的音程时更加方便。纯五度,大三度,这些都是度数。(具体度数名称下一讲会细谈)如果说半音是“厘米”的话,全音的作用就有点像大一些的“分米”,那度数就相当于“米”了。当然在一些 的音乐中存在“毫米”的概念,这样的音乐叫“微分音音乐”,但是我们在这就不做讨论了。
总结一下今天这一讲。我们首先介绍了十二平均律,这个发现解决了现代音乐中转调上的困难。然后,我们学习了如何抛开音程比例关系,转而使用抽象出来的“半音程”作为“长度”单位来衡量音程之间的“距离”。现在经过了前两讲的铺垫,你应该对半音音程这个刻度在数学上有了比一般人更深入的体会了吧?它是我们用来垒起音乐大厦的一块块砖头。
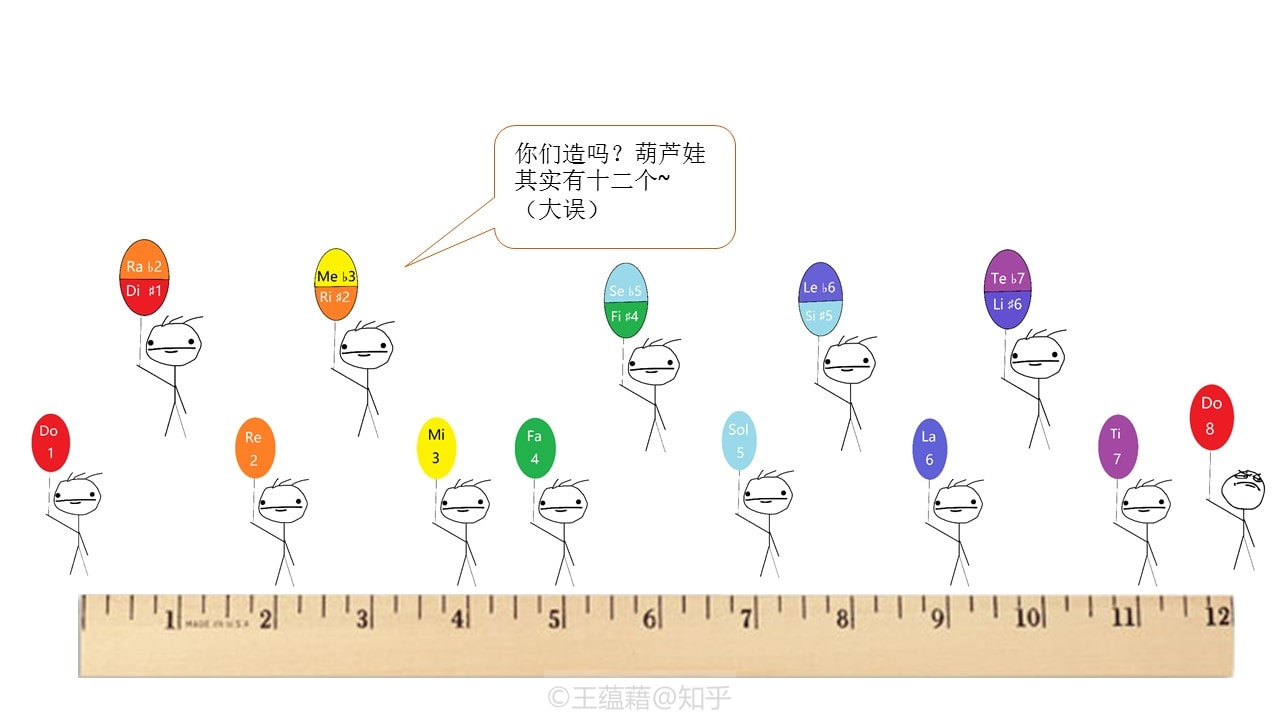
在八度的十二个音中,我们只定义了Do Re Mi Fa Sol La Ti七个音,剩下还有五个音是什么呢? 下一讲,我们会正式地命名由十二平均律发展出的十二个音和十二个音程,并让你理解英文字母ABCDEFG在音乐中的作用,以及“大”、“小”、“纯”、“增”、“减”都是什么意思。 P.S. 1. 这篇文章看完之后,除了可以尝试课后练习之外,强烈推荐大家点击下方链接进入音频演示区,用音频来直观地体验一下八度中每一个音程的协和与不协和感。你可以将它们与纯律表中的音程的音高倍数作对照,亲自感受倍数的简单程度与音程的协和性的关系。这对将来的学习大有帮助。切记,学习音乐,不能只学习乐理,同时也需要训练你的耳朵,听懂音乐,记住音乐,创造音乐。不然就沦为了纸上谈兵。 链接:【乐理101】3+. 平均律中的协和与不协和音程(上) 2. 巴赫当时使用的并不一定是平均律(Equal Temperament),而是和平均律一样便于转调的律制:优良律(Well Temperament)。平均律拥有均等的半音程,而优良律并不一定需要,定义更为宽泛。因此平均律可以理解为是优良律当中的一个特例。(“优良律”是我自己翻译的,这个词之前在国内被翻译成平均律,容易造成混淆)
Q1. 挑选2-7里面任意一个数字,立即反应出 a) 这个数字代表的唱名, b) 它上面一个音的唱名以及它们之间是全音还是半音 c.) 它的下方那个音的唱名和它们之间是全音还是半音。此训练目的是帮助牢记Mi[3]和Fa[4],还有Ti[7]和Do[8]之间是半音程关系,而其他则是全音程。
比如:数字4,唱名是Fa。上面一个音是Sol[5],Sol比Fa高一个全音。下面一个音是Mi[3],Mi比Fa低半音。 Q2. Fa到La有几个半音,他们之间是几度关系?Re和La呢?Fa和高音Mi[10]呢? Q3. 比Do高100个半音的音,理论上是哪个唱名?
Q1: Do[1]的 5/2 倍音高是高八度的哪个音,它的唱名是?那6倍音高呢,6倍音高和3倍音高之间是什么度数关系?
A1: Do[1]的五倍音高是Mi, 往下移一个八度,5/2倍也是Mi。同样,Do[1]的十倍音高也是Mi。
6倍音高和3倍是八度关系,因此是Sol。 Q2: 高八度的Fa[11],它的音高频率是原八度Do[1]的几倍?它的音高频率是原八度Fa[4]的几倍?
A2: \(\frac{4}{3}\times2=\frac{8}{3}\)倍;八度之间二倍关系。
Q3: 根据纯律的音程关系,请问Do[1]的9倍音高,15倍音高分别是什么唱名?
A3: 分别是Re和Ti。
Q4: Re[2]和Mi[3]之间的音程是什么倍数关系?
A4: \(\frac{5}{4}\times\frac{9}{8}=\frac{10}{9}\)倍;八度之间二倍关系。
约翰·塞巴斯蒂安·巴赫:Johann Sebastian Bach(常见缩写:J.S. Bach) 半音:Semitone / half step / half tone 全音:Tone / whole tone 微分音音乐: Microtonal music
在能够直觉地感觉出两个音之间孰高孰低之后,我们就应该训练更细致的听觉,习得听出两个音之间确切音程距离的能力。 当两个音同时发声时会构成一个音程,音程对人耳会产生协和或不协和感,因此每一种属性(类别)的音程都有自己的听感。我们可以把不同类别的音程在协和程度上大致划分为三个层次,分别是完全协和音程,不完全协和音程,以及不协和音程。越后面的越不协和不稳定。 在听觉上,八度最稳定,甚至是“坚硬”,以至于我都不好意思拿协和来形容了。四度在音程的稳定协和性上与五度等同,略次于八度。大三度稳定性次于四度、五度和八度,略高于大六度。大二度和大七度稳定性是最弱的,声音张力大,色彩感最强,给人一种比萨斜塔的感觉,想要倒向别的音程。每个音程有多协和,从纯律倍数关系的简单程度上我们也可以大致观察到。 1. 完全协和音程: - Do[1]与Do[1]的纯一度音程(无演示) - Do[1]与Do[8]的纯八度音程 - Do[1]与Sol[5]的纯五度音程 - Do[1]与Fa[4]的纯四度音程 2. 不完全协和音程: - Do[1]与Mi[3]的大三度音程 - Do[1]与La[6]的大六度音程 3. 非协和音程: - Do[1]与Re[2]的大二度音程 - Do[1]与Ti[7]的大七度音程 本篇我们演示了不同音程听起来都是什么样子的。想要锻炼出区分音程的能力,除了在音乐实践中锻炼之外,还可以进行专门的视唱以及练耳的锻炼。简单的流程框架可以参考Sherry Li的知乎回答:如何自学视唱练耳,有哪些循序渐进的方法?在练耳这方面,市面上有不少优秀的应用和网站帮助我们进行针对练习,比如Teoria.com,或 MyEarTraining。 视唱练耳的训练需要一定的指导和反馈,有条件应该找一位声乐老师来辅导。它往往容易被吉他学习者忽视,因为书籍视频教材中往往很少提及。但是能用耳朵理解音乐是一个音乐人的基本素养。没有锻炼出良好的听觉能力是吉他爱好者无法脱离看谱学琴的既是原因又是后果。因此,切不能忽视对耳朵的锻炼。
2. 唱名体系有两种:一种是基于大调和变化音符,另一种为每一个音都独立命名。 3. 音级可以代替唱名,用数字书写也更为便捷。 4. 吉他指板上每一品都是严格按照十二平均律制作的。
上一节课,我们通过等比关系发展出了十二平均律,有效解决了纯律变调难的问题。在平均律中,一个八度有十二个音。相邻两个音之间固定的音程被定义为半音,两个半音组成一个全音。用半音作为音程的最小单位,我们就能重新衡量并定义从纯一度到纯八度的八个音程与其对应的唱名。
在继续学习之前,请大家先回顾一下上节课的内容,确认一下你是不是已经知道Do和Re之间有几个半音,Mi和Fa之间有几个半音,Do的大三度是什么唱名了。 今天,我们沿着这个话题,继续学习平均律中的音程和唱名,搞懂唱名是怎么来的,然后带大家一起看懂吉他指板上的音高排布。 1. 自然音阶
早在平均律诞生之前,由Do Re Mi Fa Sol La Ti七个音形成的七声音阶就在欧洲的教会音乐中普及开来。由全音,全音,半音,全音,全音,全音,半音构成的这一组音程关系我们把它叫做自然音阶,是在西方古典与流行乐中最为常见的音阶。自然音阶一共有七种调式,从自然音阶的七个音中任何的一个音算起都能发展出一种新的调式音阶。比如从Re开始往上数到高八度的Re,Re Mi Fa Sol La Ti Do Re,会产生一个 全半全全全半全 的音程关系,这条音阶排列叫做 Dorian调式音阶。
随着时代的更迭,在自然音阶的七种调式中,渐渐有两种调式在使用中占了上风,成了最常用的调式。第一种叫 Ionian调式,以Do为主音,音阶向上以 全全半全全全半 排列,构成Do Re Mi Fa Sol La Ti,它后来就被大家起了一个绰号叫做“大调”(现在知道为什么Do是第一个唱名了吧?)。而第二种Aeolian调式,以La为主音,音阶向上以 全半全全半全全 排列,构成La Ti Do Re Mi Fa Sol,后来就被叫做“小调”。 音阶调式的普及就点到为止,我们会在第六课详细分析。 2. 平均律中的唱名与音程
现在说回十二平均律。十二平均律中的十二音本来应该众生平等,和Do Re Mi Fa Sol La Ti一样,拥有自己独立的唱名。然而,大调在音乐中的地位是如此不可动摇,在起名时竟也对大调中的唱名有所偏袒。这是因为基于大调的唱名在公元1000年左右就由圭多达莱佐发明了,一开始只有前六个音,唱法也和现在不一样,后来加入了Ti,变成现在这个样子。而朱载堉的十二平均律则要到1584年(明万历十二年)才被提出来,欧洲亦是在十六世纪才开始对十二平均律的探索,比唱名的诞生晚了好久,因此十二平均律中的非大调音只能和大调共享已有的唱名了。于是无奈的,出现了以下的命名法则:
我们一列一列来讲解。
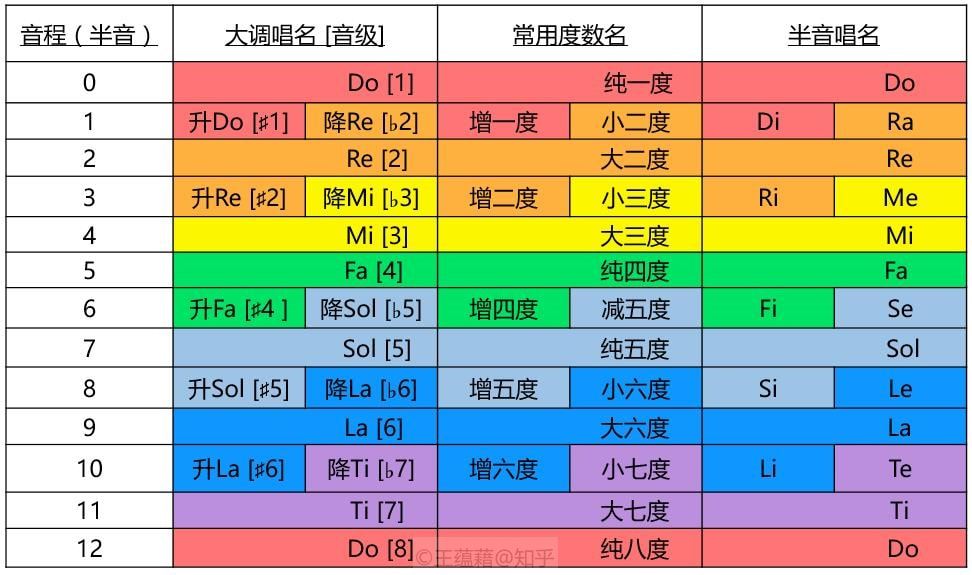
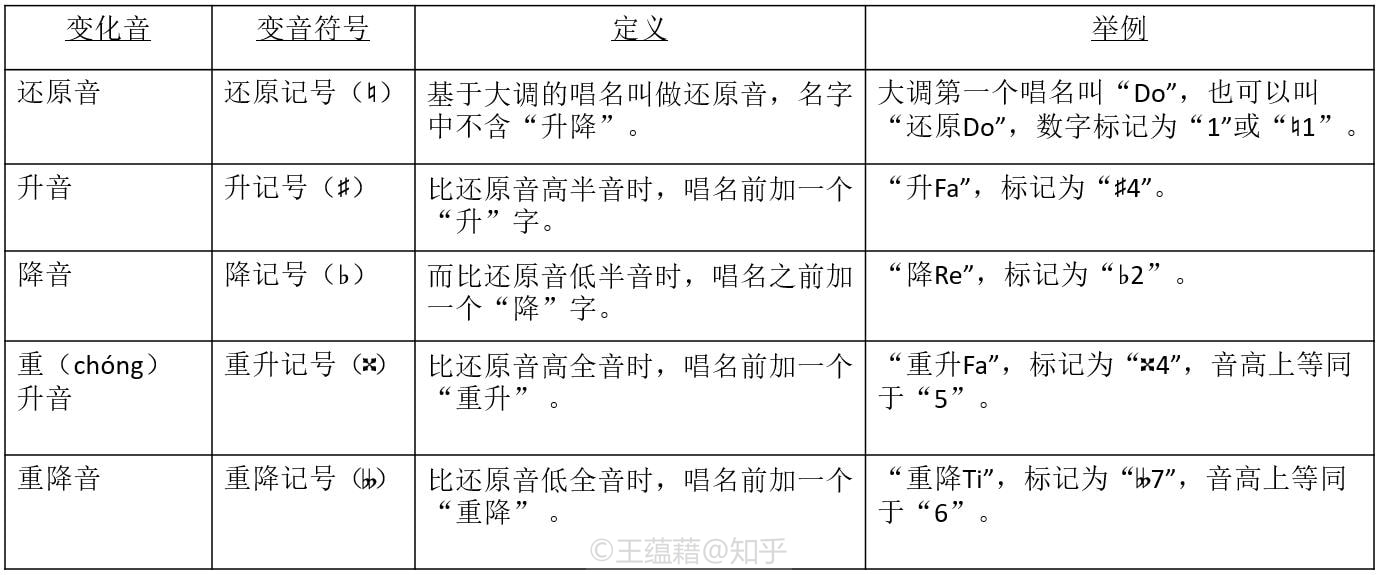
a) 大调唱名和音级 首先,根据大调音阶,我们可以分别给Do Re Mi Fa Sol La Ti标上对应的数字1-7,高一个八度的七音则为8-14,以此类推。经过了前三课,像Mi[3]这样,唱名右边方框中的数字对我们已经不陌生了,这个数字叫做大调的音级或级数。音级与唱名两相对应,当我们看到数字5时,心里面会想到“Sol”,Sol是大调的5级音。而看到9时就会想到“高八度Re”,想到高八度Re就知道是大调的9级音。由于大调音级数字与唱名是互相照应的,而且数字要比用唱名写起来更方便,我们接下来可以直接用大调的音级取代唱名来分析音乐。 小学课本里的简谱其实也是在用音级替代唱名。有所不同的是,简谱中只用到数字1-7代表大调的音,数字0代表休止不发声音。遇到升降八度时,简谱分别是在数字上方或下方加一个点来标明。 b) 变化音和变音符号 接着,介绍一下唱名的变化音和变音符号。它们的定义和例子如下:
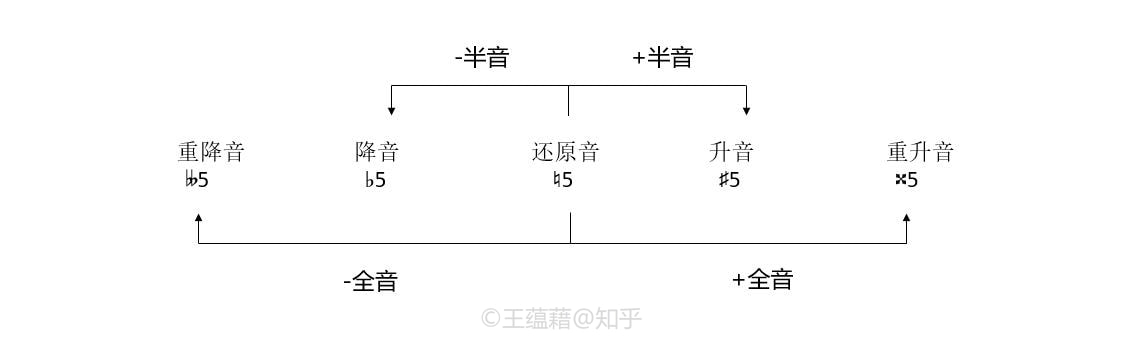
大调中未经变化的七个音1 2 3 4 5 6 7我们定义为还原音(或本位音、自然音),平均律中剩下五个非还原音都叫作变化音。还原音在音级数字不变的情况下,往上升一个半音叫升音,用♯号表示,念“升记号”。5 升一个半音得到♯5,念“升Sol”。还原音降半音得到降音,用♭号表示,念“降记号”,5 降一个半音得到♭5,念“降Sol”。还原音如果升或降一个全音,叫重升音和重降音,“重”字发音同“重复”,用×和♭♭表示。变化音的音程关系详见上图。(由于♯和♭打起来太麻烦,我接下去直接用#和b来替代,重升重降用x和bb表示)
由于十二平均律里面半音的音程均等,比1高半音又比2低半音的这个音既可以叫“#1”也可以叫“b2”,他们虽然音级和功能不同,但是在音高上是相同的音,对于演奏者来说在同一个键位。大调其他四个调外音也是如此。根据变化音符的定义,平均律中的十二个音的每个音可以同时有很多不同的名字,比如说4 = ♮4 = #3 = bb5,或者 7 = b8 = x6,但最常用的记法还是像表格里面的一样。唯一有一个例外:因为1对应着零个半音,再降就变负的了,在音乐上我们不希望出现“往上升 -1 个半音”这种诡异的沟通方式,因此1是没有降音和重降音的。当然,8是可以有降音和重降音的。
c) 音程度数
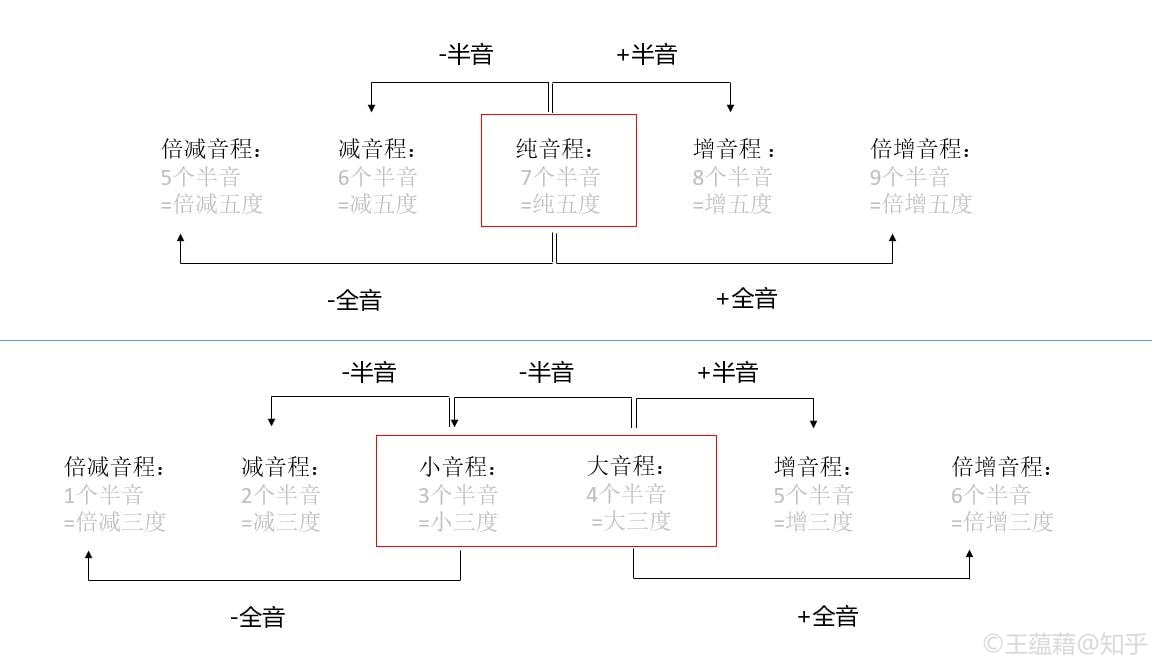
音程度数的命名也和大调结构息息相关。 以Do[1]为起点出发向上,到达大调中任何一个距离Do[1]不超过八度的音,其所构成的音程中,最为协和稳定的音程被称为纯音程,这包括了一、四、五和八度。而其余的音程都称为大音程,包括二三六七。 除了大调内的七个音,大调之外还有五个音。以Do[1]为起点出发向上,到达这五个调外音所构成的音程中,除一个例外,剩下的四个音程都可以用小音程命名:1个半音为小二度,3个半音为小三度,8个半音为小六度,10个半音为小七度。 这唯一的一个例外是由6个半音(3个全音)构成的音程。它既不是纯音程,也不是大音程或小音程,而是一个减五度或增四度。下面我们来看为什么这么命名。 同唱名有升降变化一样,音程也有不同的属性,如下图所示:
大音程减半音得小音程。小音程减半音得减音程,再减半音得倍减音程。大音程加半音得增音程,再加半音得倍增音程。而纯音程就像一个大胖子,一个人占了大小音程的位置,加减半音直接得到增减音程。这就解释了为什么纯五度下方音程为减五度,而不存在“小五度”这种错误的说法。(既然是“纯”的,那就不分“大小”了嘛。)
在音乐实践中,纯音程和大小音程的出现频率是最高的,增减音程远远次之,而倍增与倍减音程则极少会出现。对于像三度这样将音程度数区分为大与小的命名模式,其意味着着大三度与小三度在音乐中出现的比重相当。而像五度这样以纯音程命名情况,则意味着纯五度几乎占据了在五度上的唯一主导地位。因此,这样的命名并不是空穴来风。我们后续会看到,它将有效帮助我们深入理解大小调。 唱名和音程是彼此挂钩的。比如描述从1到b3的音程时我们使用“小三度”,而当描述从1到#2的音程时我们使用“增二度”。虽然两个音程大小相同都是三个半音,但是由于一个是三度一个是二度,在调式中功能会有所不同(将来会介绍),所以不能混淆着使用。 虽然彼此挂钩,但是唱名的升降和音程的增减却并不完全对应。由于自然音程中存在“纯”和“大小”这两类互相独立的音程命名模式,导致会出现以下情况:比如同样是减音程,从1到bb3是减三度,有两个降号(一个重降符号);而从1到b5是减五度,却只有一个降号。在自己推算音程与唱名音级时要格外小心。 d) 协和与不协和音程 点击这一课的课后拓展去听一听不同音程的协和度,请记住将乐理和耳朵联系在一起才是真的懂音乐。
e) 半音唱名
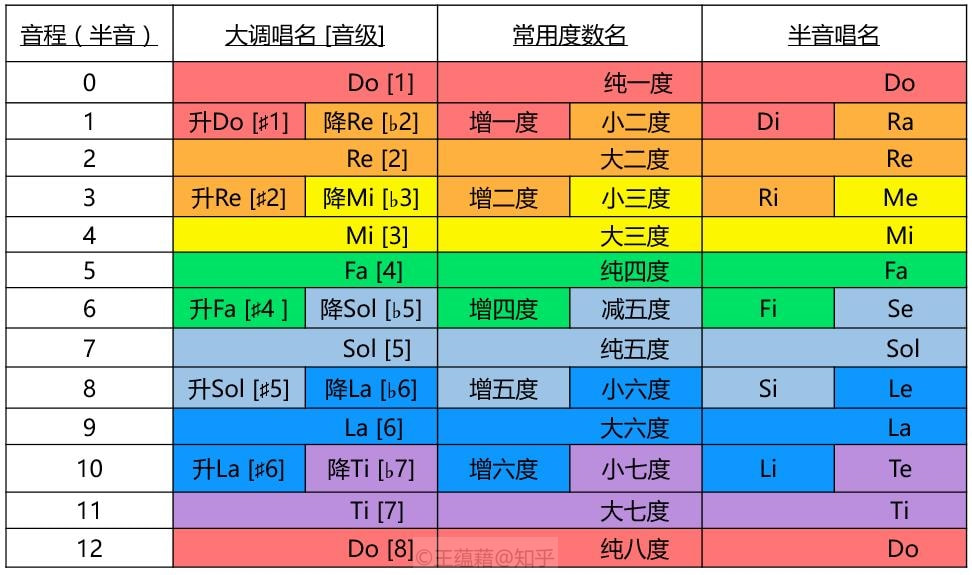
如果我们启用大调唱名系统来唱歌,会遇到一个很尴尬的事情,就是如果一个旋律恰好是,1 b7 b6 b5 b4 b3 b2 1,我们难道要跟着唱:“Do~降Ti~降La~降Sol~降Fa~降Mi~降Re~Do”?这么多降号,唱起来多费力啊!那我们不唱升降号可不可以?可以,但是万一一条旋律是 1 2 b3 3 5 1,不唱升降号就没法区分b3和3了。这对于现代大量的无调性音乐,动不动十二个音都用的曲子来说,简直是一场噩梦。 为了简化平均律上十二个音的唱名,大约上世纪初(求大神求证科普),出现了一套每个唱名都只有一个音节的系统叫做半音唱名法,与上文介绍的大调唱名法有所不同。我们从Do Re Mi Fa Sol La Ti中抽取出D R M F S L T七个辅音,比还原音高半音时(升音),在辅音后加上元音 i;在比还原音低半音时(降音),在辅音后面加上元音 e(Re还原音本身就跟着e,所以降Re改叫Ra)。比如升Fa可以改写为由 F 和 i 组合出 “Fi” 这个唱名,降Mi则可以改写为由 M 和 e 组成的 “Me”。根据这个规则,我们就得到了第一张表中的所有半音唱名。这套唱名用于爵士这类变化音多的音乐就非常的合适。 (升Sol可以改写为Si。而Si在国内音乐教材中指的是大调的七级音,会产生避免混淆。这就是为什么我们要把七级音叫成Ti。) 3. 吉他指板简介
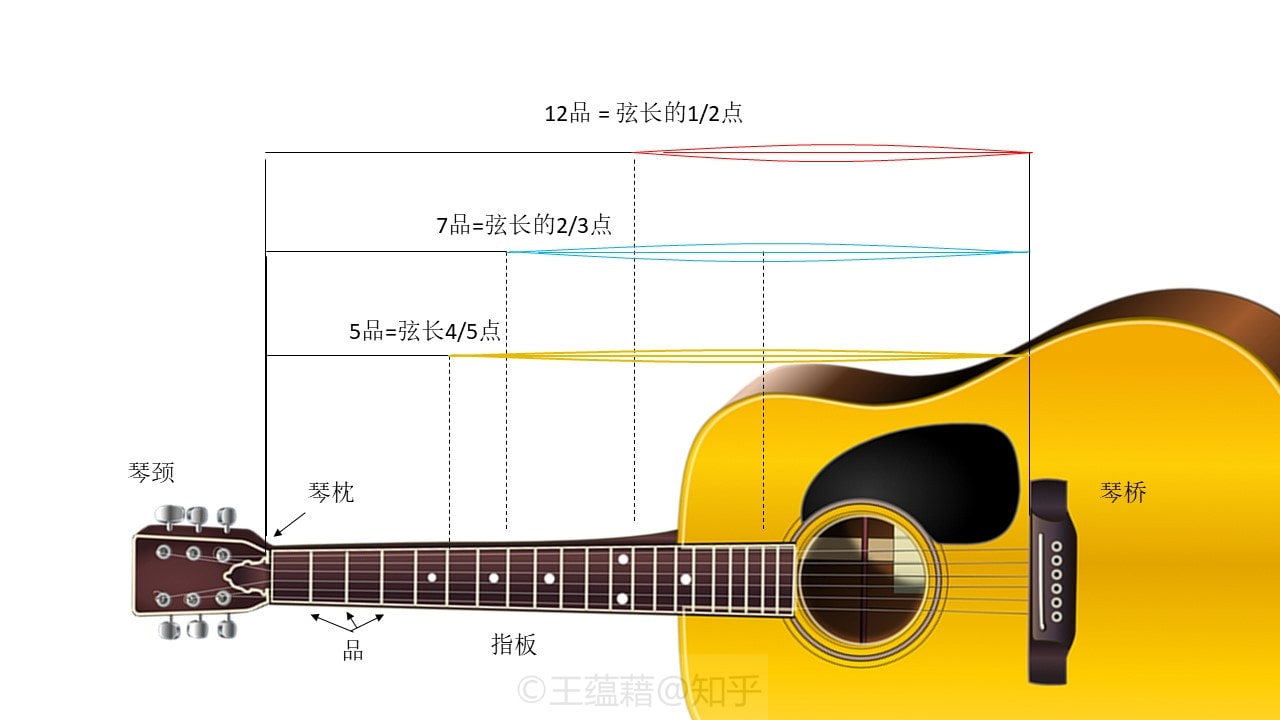
最后,我们来简单介绍一下吉他的指板,看看十二平均律是如何在吉他上体现的。吉他发声靠的是琴弦振动,振动传递到共鸣箱后扩大了振动表面的面积,使音量得到扩大。学过高中物理的同学可能还记得,同样张力的琴弦,当弦长缩短到原来的1/n时,振动频率就会升高到原来的n倍。因此,吉他手可以将手指按在吉他指板上凸出的品丝,来缩短弦的振动长度,从而升高琴弦发出的音。在左手不按品丝,右手直接拨响琴弦时,琴弦所发的音叫“空弦音”,弦的振动长度是从琴枕到琴桥的距离。
由于弦长和音高频率成反比,当振动弦长缩短一半时,音高正好高了一倍。说到二倍音高,我们会想到什么?对,八度!吉他从琴颈往琴桥数,第十二品的位置正好是弦长的二等分点。当我们把手指按在十二品上时,弦长振动长度缩短一半,我们就得到了比空弦音高了一个八度的音。换句话说,空弦到十二品正好是一个八度。
吉他是一个严格的十二平均律乐器。十二平均律将八度分为十二等份,而吉他一个八度间也有十二个,相邻两品之间都是半音关系,完全遵循十二平均律。于是当我们手指按在七品时,弹奏的音高比空弦高了7个半音,即纯五度。根据上一讲知识,我们知道十二平均律中纯五度的音程倍数\(2^\frac{7}{12}\)近似于纯律中的3/2倍。也就是说,七品的位置应该正好能在按弦时将弦长振动范围缩短为空弦的近2/3倍。这与我们的目测是一致的。
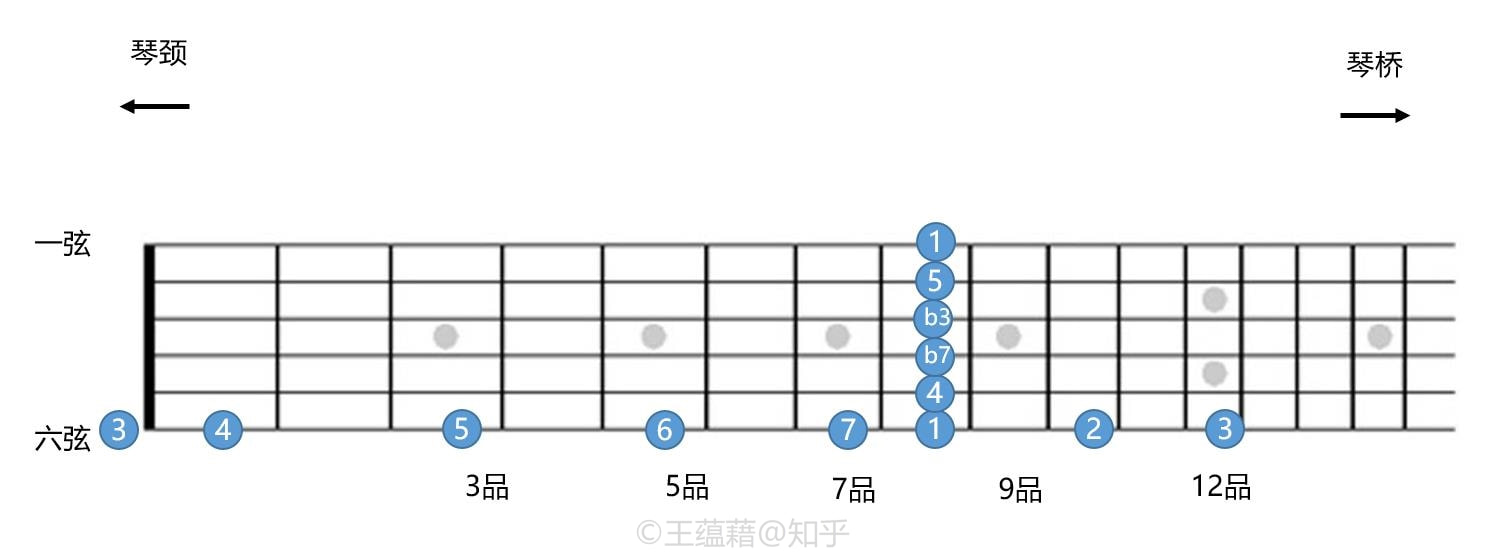
吉他一共有六根弦,每根弦都符合上述的规律。六根弦由细到粗分别由数字一到六标注,一弦最细,六弦最粗。拿六弦举例,若以八品为1,那么十二品和空弦就都是3。从空弦到十二品正好是一个八度循环。十三品到二十四品之间,音的排列和一品到十二品是一模一样的。十三品的音同一品一样都是4,只是音高上高了八度。
了解了吉他单根弦上面的音程关系,我们再看一下跨弦间的音程关系。同一品上,五弦比六弦高5个半音,四弦比五弦高5个半音,三弦比四弦高5个半音,二弦比三弦高4个半音,一弦比二弦高5个半音。因此,同一品的五弦比六弦高5个半音,即四度。四弦比六弦则高出了5+5=10个半音,相当于小七度。三弦上的音则比六弦高出5+5+5=12+3个半音,相当于八度加小三度。二弦上的音比六弦高出5+5+5+4=12+7个半音,即八度加五度。最后,一弦比六弦高了5+5+5+4+5=24个半音,即两个八度。所以如上图,如果以六弦八品为1,我们就能算出从六弦到一弦八品上的音分别是 1 4 b7 b3 5 1(考虑八度关系的话是1 4 b7 b10 12 15)。 有了纵向与横向的音程关系,通过数格子加减半音就可以推算出整个指板上所有的音程关系和唱名音级了。了解了吉他的指板原理,你对平均律是不是又有了进一步的认识呢? 总结一下,今天我们命名了平均律上所有的唱名、音级与音程,并在吉他指板上演示了平均律。期间介绍了两套唱名,并提到唱名可以升降还原,音程则分大小增减纯。下一讲,我们将介绍音名的概念,并带你参观钢琴的琴键。
Q2: 列出所有两个音程相加等于纯五度的音程组合 Q3: 自然音阶中,哪七对唱名(或音级)之间是五度关系,是纯五度还是减五度? Q4: 自然音阶中,哪七对唱名(或音级)之间是三度关系,是大三度还是小三度? Q5: 任意挑选平均律中的两个音,说出它们的音程关系。
Q2: Fa到La有几个半音,他们之间是几度关系?Re和La呢?Fa和高音Mi[10]呢?
A2: Fa到La有4个半音相当于大三度。Re到La有7个半音相当于纯五度。Fa到Mi有11个半音相当于大七度。
Q3: 比Do高100个半音的音,理论上是哪个唱名?
A3: 100 = 12*8+4 => 因为12个半音是八度,4个半音是大三度。因此比Do高100个半音的音是升了8个八度的Mi。
音阶:Scale 调式:Mode 半音唱名法:Chromatic solfege 大调唱名法:Diatonic solfege 音级:Degree 音程:Interval 增和倍增(音程):Augmented and doubly augmented (intervals) 减与倍减: Diminished and doubly diminished 大: Major 小: Minor 纯: Perfect(在台湾翻译为“完全”,比如“完全五度”) 变音记号: Accidentals 还原:Natural 升与重升:Sharp and double sharp 降与重降:Flat and double flat 三全音:Tritone
琴桥:Bridge 琴颈:Neck 琴枕:Nut 琴弦:String 品:Fret 指板:Fretboard
【好和弦】八分鐘以內,一次搞懂音程名稱!-在线播放-优酷网,视频高清在线观看 2. Quora帖子:关于自然音阶是如何在西方音乐中占领主导地位的 When and why did the diatonic scale become so important in Western music? |
王蕴藉@知乎吉他乐理老师,《乐理101》、《吉他恋爱手札》专栏作者 目录
All
|


 RSS Feed
RSS Feed